¿Cuántos triángulos hay en el techo del Movistar Arena?

¡Retomamos los análisis chungos en este blog!

Para responder la pregunta ¿Cuántos triángulos hay en el techo del Movistar Arena de Santiago de Chile? necesito antes contarles sobre la última vez que me sentí verdaderamente inteligente. Fue hace 23 años, en una clase de preuniversitario a la que asistíamos alumnos de distintos colegios del pueblo. Uno de mis profesores planteó un desafío: “¿Cuántos cuadrados hay en un tablero de ajedrez?”

Un compañero, algo distraído preguntó si eran infinitos. Ante esto, el profesor nos dio una pista: “Son más de 100, pero menos de 300”. Luego, otro compañero, bastante arrogante y de otro colegio, sugirió que eran 256. Al recibir una respuesta negativa, corrigió su estimación a 128, pero tampoco era correcto. Finalmente, llegó mi turno. Con seguridad respondí: “204”. Mi respuesta provocó una sonrisa del profesor, quien confirmó que esa era, efectivamente, la respuesta correcta.

Años antes, en uno de los libros de mi casa, Mi primer libro de BASIC, leí la historia de Carl Gauss y cómo, siendo un niño, su profesor intentó castigarlo pidiéndole que sumara todos los números del 1 al 100. Para sorpresa de todos, después de unos pocos minutos, Gauss volvió con la respuesta correcta: 5050. Había descubierto un patrón que le permitió resolver rápidamente un problema que, en apariencia, era tedioso y largo.

Aunque no existe evidencia histórica de que esta anécdota haya ocurrido realmente, este tipo de historias hacen que las matemáticas se sientan más humanas y accesibles. Por eso, elijo creer que sí sucedió. Y al recordar esa historia, decidí buscar un patrón para descubrir cuántos cuadrados hay en el tablero de ajedrez. Comencé identificando que había 64 cuadrados de 1×1 y solo 1 cuadrado de 8×8. Luego noté que había 4 cuadrados de 7×7.

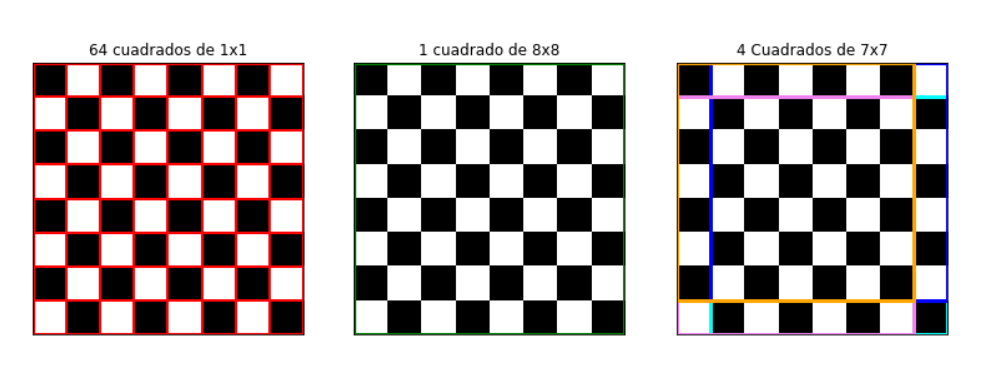
Con esta observación, pude deducir el patrón y encontrar la fórmula que me permitió resolver el problema:

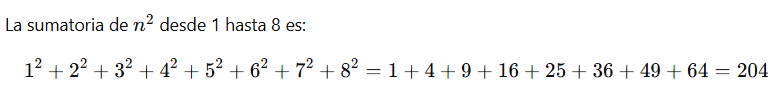
Muchos años después, frente al pelotón de fusilamiento, miré el techo del movistar Arena y dije… ¡son hartos, pero debe haber un patrón!

Primero miré el centro y vi que habían 8 triángulos dentro del primer grupo:

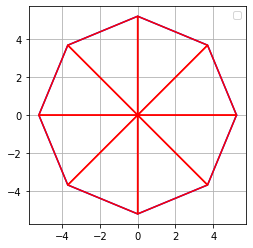
Luego, al ver el siguiente grupo para cada triangulo anterior(rojo), ahora hay 4 triángulos (uno rojo y tres morados), con lo que el total de triángulos son 8×4=32.

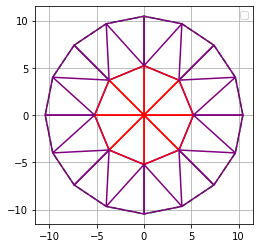
En el siguiente grupo serán 9 (uno rojo, tres morados y cinco naranjos), y el total de triángulos 8×9=72.

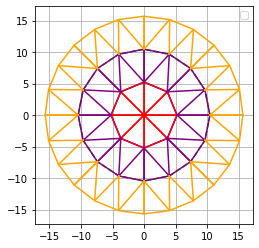
Con ello, basta contar que son 18 grupos y el resultado será:

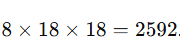
Así que ya saben. La próxima vez que estén disfrutando de su espectáculo favorito sepan bien que hay 2592 triángulos esperando a caer sobre nuestras cabezas, por Tutatis.